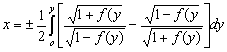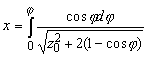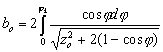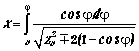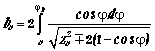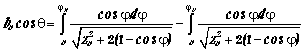|
For the first time main
equation of the theory of capillary attraction circumscribing the form
of an equilibrium surface of a capillary fluid in a field of gravity,
for the analysis of weld formation during arc welding is applied by Voloshkevich
G.Z. in [Ref.377].
Having written it for a cylindrical surface of a welding pool as follows
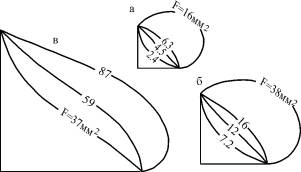
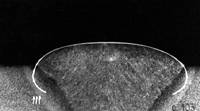
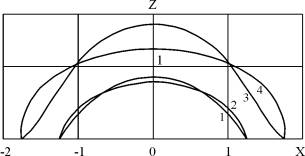
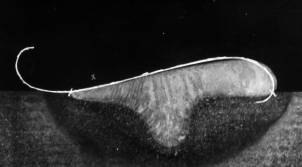
author [377] by a method of graphic integration had obtained the set of integral curves of this equation circumscribing the form of a surface of welds, forming at arc welding in different positions. Having imposed an appropriate curve on the profile of real fillet weld, Voloshkevich G.Z. has received good enough correspondence of the calculated and real forms of the weld ( Fig.1). |
|
||||||||||||||||||
|
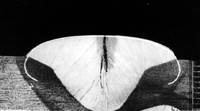
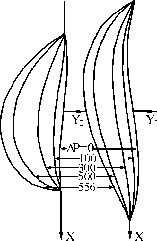
The
solution of the equation (1) in quadratures for calculation of the bead
shape in a flat position, had obtained Emelyanov
I.L. in 1972 year [471]. In this solution the equation of a integral curve for the profile
of a weld is written as follows
where h - height of
the weld; Ro - curvature radius in the top of a weld. All
calculations were fulfilled in [471] for concrete value of a capillary
stationary value àê=23.2 ìì2. |
Fig. 2 |
||||||||||||||||||
|
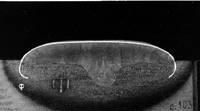
In
1975-1976 Nishiguchi
K. [474,475]
had obtained a solution of the equation (1) as follows
where the function f (y) is determined by an expression
This solution utilised also for the description of the shapes of fillet welds at a position «in corner» and horizontal welds on a vertical plane [474, Nishiguchi K., 1976]. In fig.3 the comparison of calculated and experimentally obtained weld's shape is exhibited. |
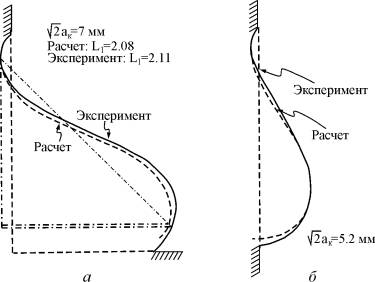
Fig.3 |
||||||||||||||||||
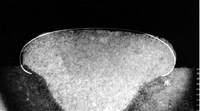
In
1977 Berezovsky B.M.
[479] had obtained a solution of the equation (1) in more convenient
parametric kind
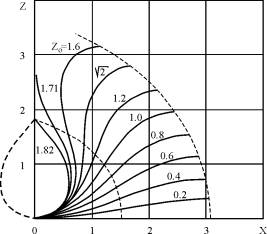
That had allowed to find complete closed system of the equations linking main geometrical parameters of weld reinforcement (deposited bead)
where
where B,C -
width and height of weld
reinforcement,
mm; Z0 - parameter of curvature, mm; Fí - square
of a weld metal, ìì2. |
Fig.4
|
||||||||||||||||||
In 1979 Berezovsky
B.M.
[667] has applied the given approach to mathematical modelling of
creation of a seam in a ceiling position and has received solution by
the way
And the lower
sign takes at build-up of an integral curve circumscribing the form of
convexity of a seam in a lower position, and upper sign - in a ceiling
position.
And the upper sign
corresponds(meets) to a ceiling position, and lower sign - lower
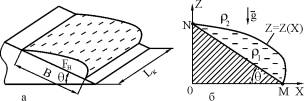
position. Experimental check of model of weld formation in overhead positions For check of the obtained designed equations the experiments on a surfacing of cylinders in a ceiling position were conducted. The surfacing was produced by electrodes with different types of coatings of brands ÌÐ-3, ÀÍÎ-4, ÎÇÑ-4, ÓÎÍÈ-13/55 a dia of 4 mms on slices from mild become a size 400õ200õ10 mm. As the power supply have utillized a welding rectifier VDU-504. With the purpose of exception of the factor of qualification of the welder (or with reference to conditions of automatic welding) a surfacing realized on an automaton ADS-1000-2, equipped by special accommodating for welding by the plated electrodes (Fig. 6.13).
|
|
||||||||||||||||||
|
In 1983 Berezovskii
B.M.
[482] had applied the given approach to mathematical modelling of
horizontal welds on a vertical plane, and in 1988 - on an inclined plane
[480].
For this
scheme obtained
the follows equations:
|
|
||||||||||||||||||
|
The author of [484]
experimentally and theoretically had studied weld formation in a flat
and overhead positions. The physical analog of this model had
represented by the two slices, between which backs the fluid phase is
posed. For the analysis of the process of root weld formation the
capillary-hydrostatic model for a special case was built, when width of
a root seam Â1 and width it
Â2 are identical. In the paper [485] the model explaining a reconfigurating of a welding pool at welding of thin metal with burning through on weight in different space positions is offered. For obtaining equilibrium equations of weld pool surface the variational energetical method was utilised which has allowed not only to obtain the equilibrium form of a through seam at its shape in different positions, but also to estimate stability of a surface of a fluid phase between hard ridges. |
|
||||||||||||||||||
| References
377. Voloshkevich G.Z. Welding of vertical seams by a method of forced formation // The Anniversary issue dedicated 80-years of E.O.Paton. - Kiev: Ukraine Sciences Academy Publishing, 1951. p.p. 371-395. 471. Emelyanov I.L. Effect of surface tension forces and external pressure on the shape of a deposited bead // Trans. of Leningrad Institute of Water Transport. - 1972, Vol.135. - p.p.135-145. 472. Emelyanov I.L. Effect of surface tension forces on the shape of fillet welds // Trans. of Leningrad Institute of Water Transport. - 1973, Vol.142. - p.p.120-126. 474. Nishiguchi K., Ohji T., Matsui H. Fundamental research on bead formation in overlaying and fillet welding processes ( Report 1). Surface tensional analysis of bead surface profile // J. of the Jap. Welding Soc. - 1976, Vol.45. - No.1. - P.82-87 ( jap.) 475. Nishiguchi K. Fundamental researches on bead formation in overlaying and fillet welding process ( 2nd Report ). Surface tensional analysis of surface profile of horizontal fillet weld // J. Jap. Welding Soc. - 1976, Vol.45. - No.2. - P.143-149 ( jap.) 479. Berezovskii B.M., Stikhin V.A. Influence of forces of surface tension on formation of reinforcement of weld.// Welding Production — 1977. — No. 1. — p.p. 51—53. Berezovskii B.M., Stikhin V.A. Calculated definition of weld reinforcement shape and critical dimensions of weld pool at overhead welding // Proceedings of Chelyabinsk Polytechnical Institute. — Vol.207. — 1979.— p.p.103-111. 480. Berezovskii B.M. Mathematical modelling of weld formation on a inclined plane // Automatic Welding. — 1988. — ¹1. — p.p.26—31. 482. Berezovskii B.M., Suzdalev I.V., Stikhin V.A. et al Mathematical modeling and optimising of weld formation on vertical plane // Automatic Welding. — 1983. — No.3. — p.p.21—24. 484. Kureishi M. Correlation among parameters affecting on the formation of penetration beeds // J. of the Jap. Weld. Soc. - 1980, Vol.49. - ¹5. - P.297-304. (jap.) 485. Andrews J.G., Atthey D.R., Byatt-Smith J.G. Weld pool sag // J. of Fluid Mech. - 1980, Vol.100. - No.4. - P.785-800. |
|||||||||||||||||||
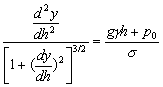 ,
(1)
,
(1)
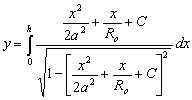 ,
(2)
,
(2)